شهد العقد الماضي تسارعًا هائلاً في إمكانات البرمجيات على حل مشاكل معقدة أكثر من أي وقت مضى، منتجات مثل Siri و Google Translate ومجالات مثل معالجة اللغة والتعرف الآلي على محتويات الصور لم تكن ممكنة لولا التقدم السريع في تقنيات تعلم الآلة والذكاء الاصطناعي، هذه التقنيات حققت تحولًا نوعيًا في جودة الحلول البرمجية وغيّرت طريقة بناء البرمجيات.
على سبيل المثال تخيل برنامجًا لتحويل مقطع صوتي إلى نص، في السابق كنت ستحتاج إلى فريق ضخم من المختصين باللغويات، وبرنامجًا معقدًا مكونٌ من نصف مليون سطر برمجي؛ لكن بعد التطورات الحديثة في مجال تعلم الآلة، أصبح الأمر ممكنًا ببرنامج قد لا يتجاوز مئة سطر برمجي، يقوم ببناء شبكة عصبونية تتعلم من كمية كبيرة من البيانات، لتحقق نتائج أقل خطئًا وأكثر دقة وصحة من البرامج الضخمة السابقة.
هذه المقالة هي مقدمة مبسطة إلى الشبكات العصبونية (Neural Networks) والتي تشكل حجر الأساس لأغلب حلول تعلم الآلة والذكاء الاصطناعي.
لنبدأ بمثال بسيط: أراد صديقك أن يشتري منزلًا، وقال إنه سعّر منزلًا مساحته 200 قدم مربع (ما يعادل 185 متر) بـ 400,000 دولار. فهل هذا سعر جيد أم لا؟
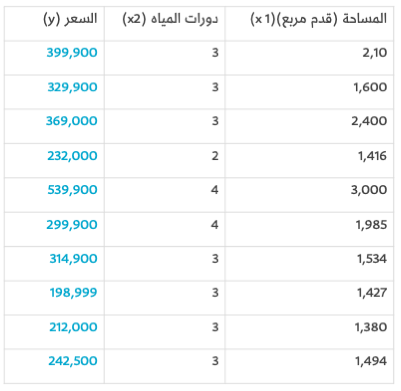
ليس من السهل التقييم دون إطار مرجعي. لذا ستذهب وتسأل ثلاثة من أصدقائك الذين اشتروا منازل في تلك الأحياء نفسها عن أسعارها، لتصبح لديك نقاط البيانات التالية:
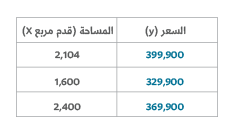
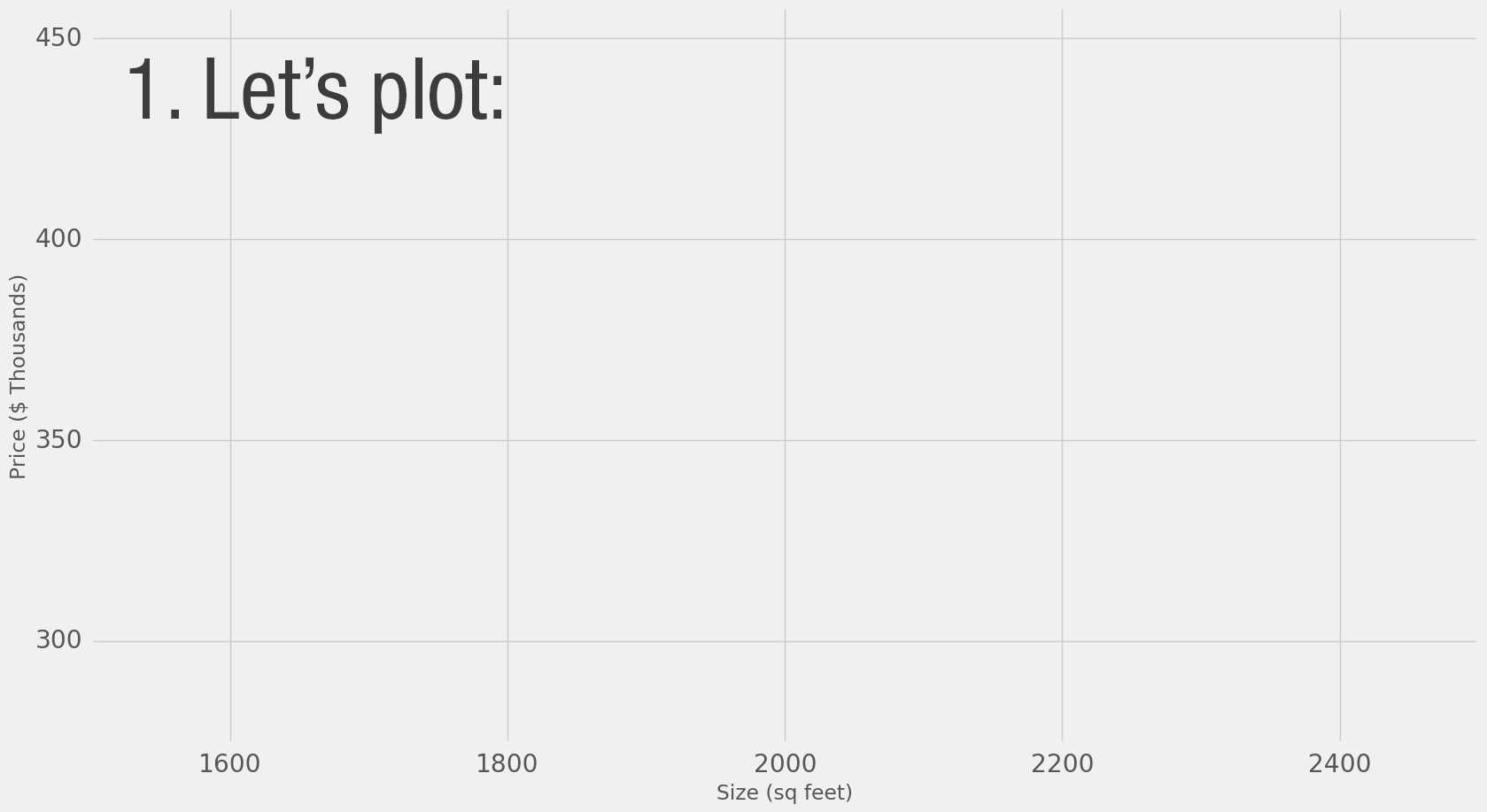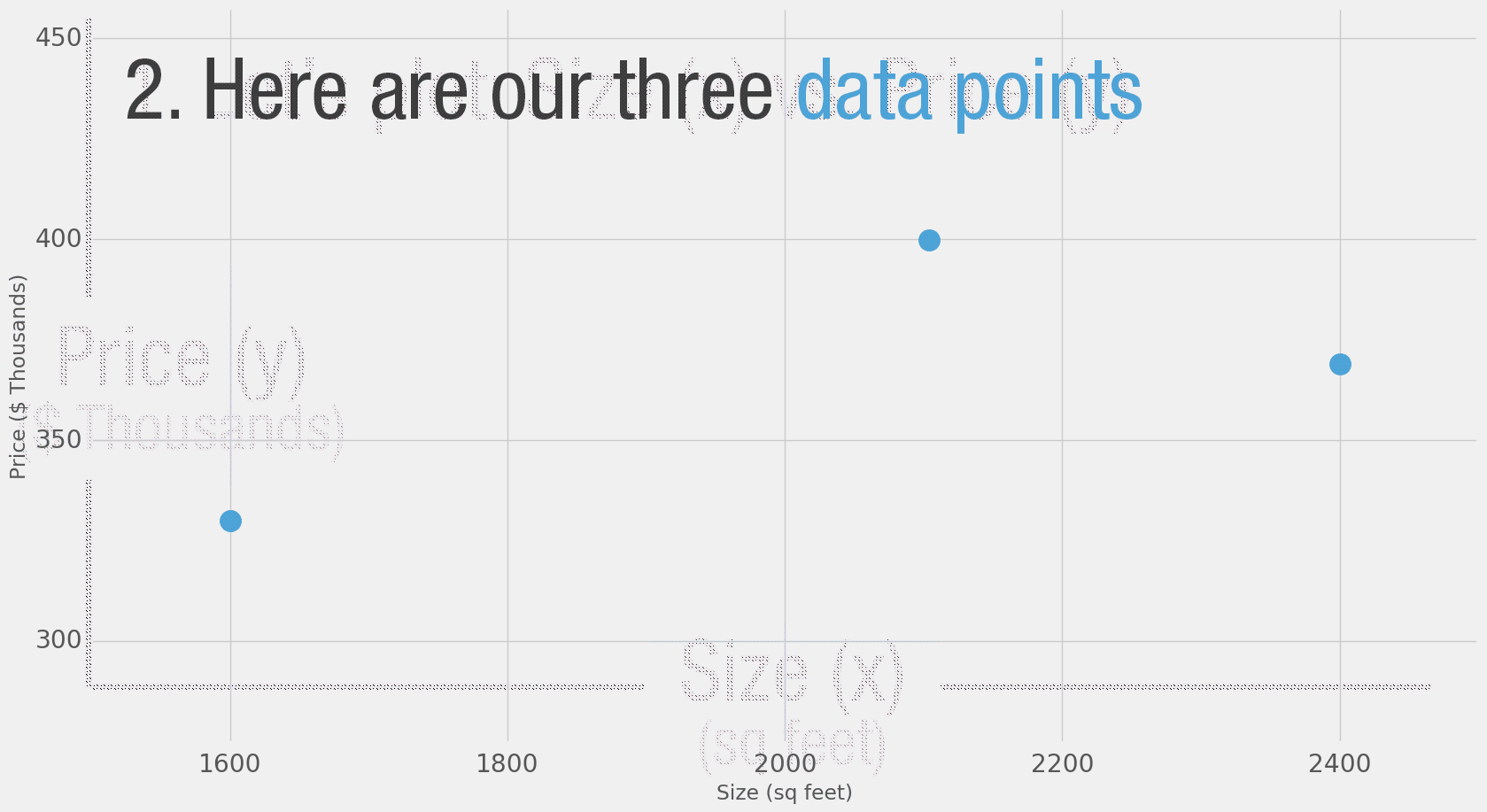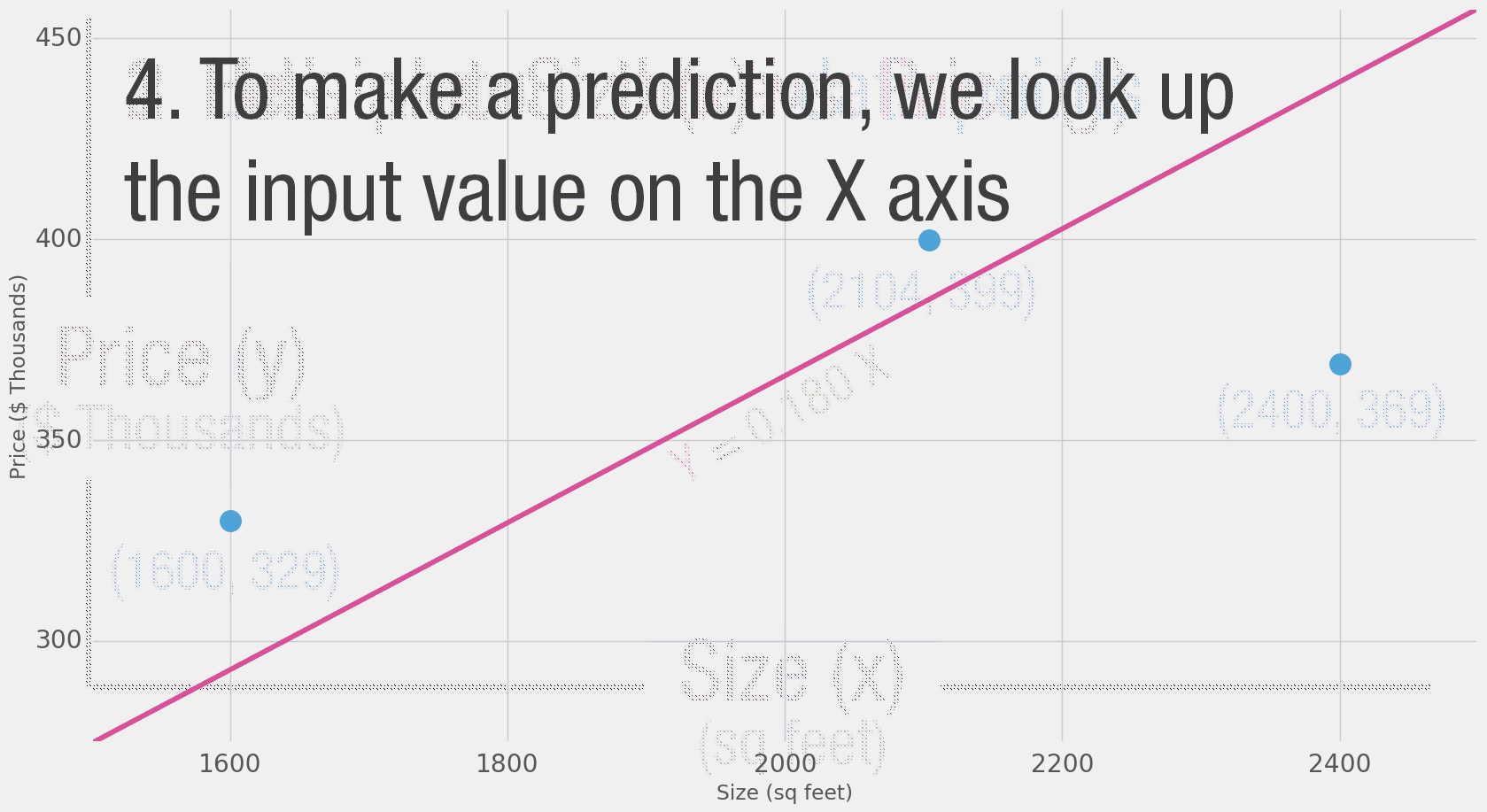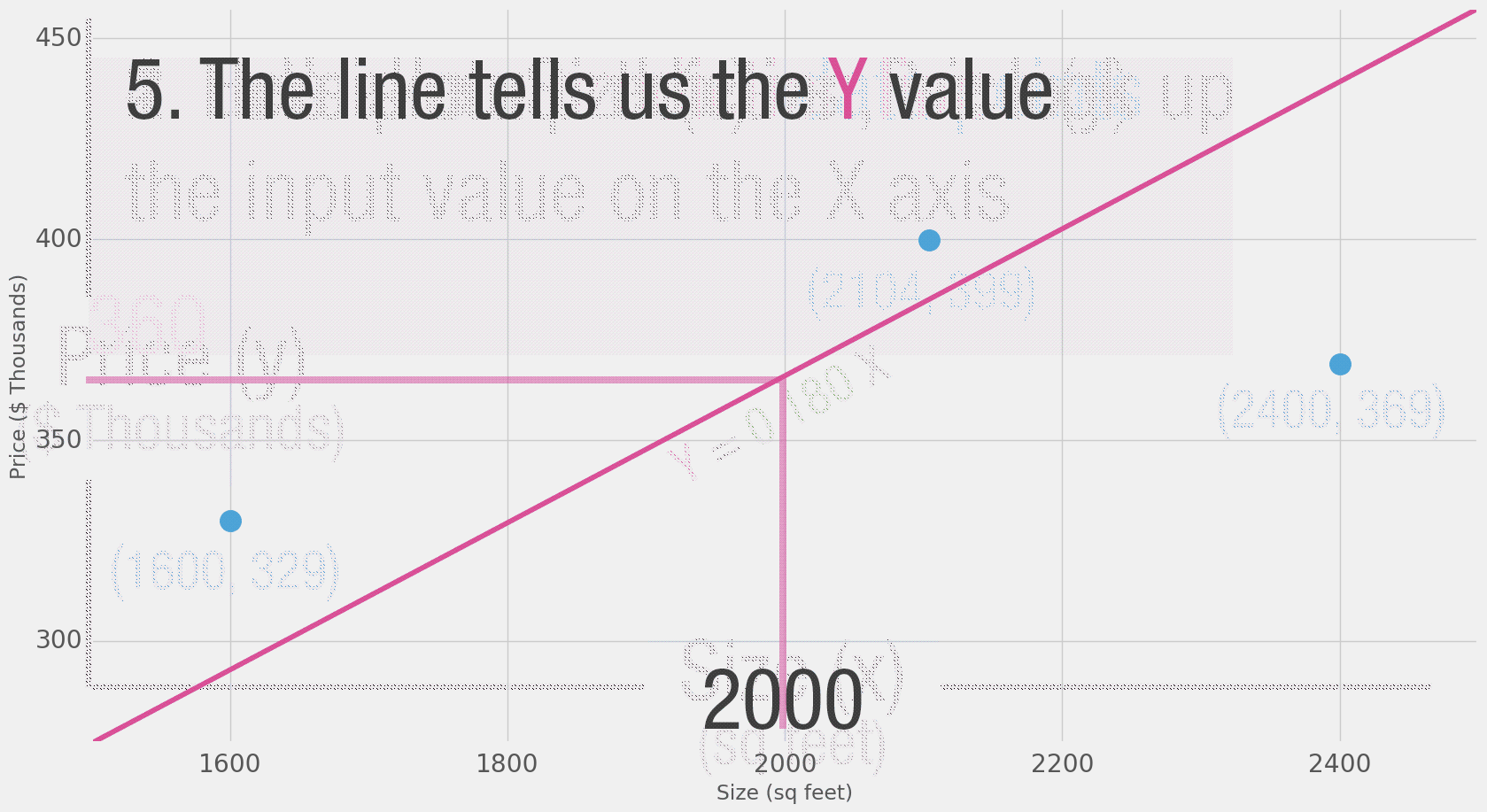
شخصيًا، أول حل يرد إليّ هو معرفة متوسط سعّر القدم المربع، وهو هنا 180 دولار للقدم المربع الواحد.
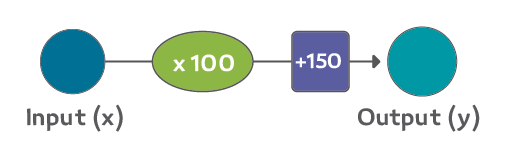
مرحبًا بك في شبكتك العصبونية الأولى! هي حتمًا ليست في مستوى Siri لكنك الآن تعرف الركيزة الأساسية. وهذا شكلها المبدئي:

توضح لك المخططات من هذا النوع هيكل الشبكة وكيف تقوم الشبكات بحساب التوقع. يبدأ الحساب من وحدة الإدخال على اليمين، وتتدفق قيم المدخلات نحو اليسار، تضرب بالوزن والناتج يصبح المُخرج.
ناتج ضرب 2000 قدم مربع في 180 هو 360,000 دولار، هذا كل ما في الأمر في هذه المرحلة. حساب التنبؤ هو عملية ضرب بسيطة، ولكن قبل ذلك، علينا التفكير في الوزن الذي سنضرب به. في هذا المثال بدأنا بمتوسط المعدل، ولكن لاحقًا سننظر في خوارزميات أفضل من الممكن أن تزداد كلما حصلنا على المزيد من المدخلات ونماذج أكثر تعقيدًا. إن العثور على الوزن الآن يعد مرحلة تدريب. لذلك إن سمعت في وقت لاحق عن شخص "يدرّب" شبكة عصبونية، فهذا يعني محاولة إيجاد الأوزان التي نستخدمها لحساب التنبؤ.

هذا شكل من أشكال التنبؤ البسيطة التي تأخذ مدخلات، وتقوم بالحساب وتعطينا الناتج (وبما أن الناتج يمكن أن يكون ذا قيم مستمرة، فإن الاسم التقني لما لدينا سيكون "نموذج إنحدار")
دعونا نتصور هذه العملية (باختصار، سنقوم بتبديل وحدة السعر لدينا من 1 دولار إلى 1000 دولار. الآن وزننا هو 0.180 بدلًا من 180):
أصعب، أفضل، أسرع، أقوى
هل يمكننا القيام بعمل أفضل من تقدير السعر بناءً على متوسط نقاط البيانات لدينا؟ دعنا نحاول، لنحدد أولًا ما قد يكون خيارًا أفضل في هذا السيناريو، إن قمنا بتطبيق النموذج على نقاط البيانات الثلاث التي لدينا، فما مدى جودته؟
Missing GIF
هنالك بعض الأصفر، وهذا لا يعني أمرًا جيّدًا لأنه يعني وجود أخطاء، لذلك علينا تقليص الأصفر بقدر ما نستطيع.
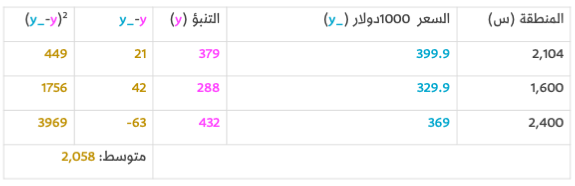
هنا يمكننا أن نرى القيمة الفعلية للسعر، وكذلك قيمة السعر المتوقع، والفرق بينهما، سنحتاج الآن لحساب متوسط هذه الفروقات حتى يكون لدينا رقم يخبرنا عن مقدار الخطأ في نموذج التنبؤ هذا. الإشكالية هنا هي أن الصف الثالث تتواجد فيه "-63" كقيمة سالبة، علينا التعامل مع هذه القيمة السالبة إن أردنا استخدام الفرق بين القيمة المتوقعة للسعر وقيمة السعر الفعلي كمقياس للخطأ. لذا سنضيف خانة إضافية فيها تربيع الخطأ، وبالتالي نتخلص من القيمة السالبة. هذا هو تعريفنا الآن للقيام بالعمل بشكل أفضل – والنموذج الأفضل هو النموذج الذي يحتوي أخطاء أقل. يتم حساب الخطأ بقياس متوسط أخطاء كل النقاط في مجموعة البيانات. لكل نقطة، يقاس الخطأ بالفرق بين القيمة الفعلية والقيمة المتوقعة ورفعها إلى الأس 2. وهذا ما يسمى بالجذر التربيعي لمتوسط مربع الخطأ. يمكننا استخدامه كدليل لتدريب نموذجنا بجعله دالة الخسارة (أيضًا، دالة التكلفة).
الآن بعد أن حددنا عصا القياس الخاصة بنا لجعل النموذج أفضل، لنجرب بضعة قيم للوزن ومقارنتها بمتوسط اختيارنا:
Missing GIF
يمكن لهذه الخطوط تقريب القيم بشكل أفضل الآن بعد أن أصبح لدينا هذه القيمة b المضافة إلى صيغة الخط.
وفي هذا السياق، سيتم تسميتها "تحيز". وهذا يجعل شبكتنا العصبونية تبدو هكذا:
يمكننا تعميمها بالقول إن الشبكة العصبونية ذات المدخل الواحد والمخرج الواحد (تنويه: دون طبقات مخفية) تبدو هكذا:
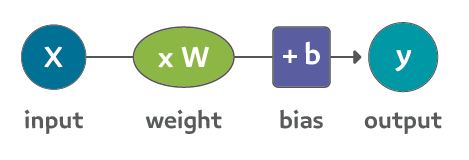
في هذا الرسم البياني، W و b قيم تم إيجادها اثناء عملية التدريب، X هي المدخلات التي سيتم إدراجها بالمعادلة (يتم حساب المساحة بالقدم المربع في هذا المثال). Y هو السعر المتوقع.
سيتم الآن حساب التنبؤ باستخدام هذه الصيغة

لذا فإن نموذجنا الحالي يحسب التنبؤات عن طريق التعويض عن مساحة المنزل بـ x في هذه الصيغة:

ما رأيك أن تجرّب يدك في تدريب شبكتنا العصبونية؟ بتخفيف حدة الخسارة عن طريق تحديد الوزن والتحيز. هل يمكنك الحصول على قيمة خطأ أقل من 799؟ جرّب هنا
تهانينا، لقد قمت للتو بتدريب شبكتك العصبونية الأولى يدويًا! فلنلقي نظرة على كيفية أتمتة هذه العملية. فيما يلي مثال آخر مع وظيفة إضافية تشبه الطيار الآلي. هذه هي أزرار Step GD، تستخدم خوارزمية تسمى "الانحدار المتدرج" لمحاولة مقاربة الوزن الصحيح والقيم المتحيزة التي تقلل دالة التكلفة إلى أدنى حد.
بإمكانك استخدام هذان الرسمان البيانيّان الجديدان لمساعدتك في تتبع قيم الخطأ أثناء تغييرك لمعايير (الوزن والتحيز) النموذج. ومن المهم تتبع الخطأ لأن عملية التدريب تتمحور حول تقليله قدر الإمكان.
كيف يمكن لتدرج النسب معرفة خطوته التالية؟ عن طريق حساب التفاضل والتكامل. فكما ترى، عند معرفة الدالة التي نقوم بتقليلها (دالة الخسارة، ومتوسط y_ - y) ²) لجميع نقاط البيانات التي لدينا)، وبمعرفة المُدخلات الحالية (الوزن الحالي والتحيز)، فإن مشتقات دالة الخسارة ستخبرنا بأي اتجاه يمكن أن ندفع W و b حتى نتمكن من تقليل الخطأ إلى أدنى حد.
تعلّم المزيد عن الانحدار المتدرج وكيفية استخدامه لحساب التحيز والأوزان الجديدة في المحاضرات الأولى لدورة التعلم الآلي على Coursera.
وبعد ذلك، أصبحا اثنان
هل حجم المنزل هو المتغير الوحيد الذي يدخل ضمن تكلفته؟ من الواضح أن هنالك العديد من العوامل الأخرى. لنُضف متغيرًا آخر ونرى كيف يمكننا ضبط شبكتنا العصبونية بناءً عليه.
لنفترض أن صديقك أجرى بحثًا بتوسع أكبر، ووجد مجموعة بيانات تكتشف أيضًا عدد دورات المياه في كل منزل:
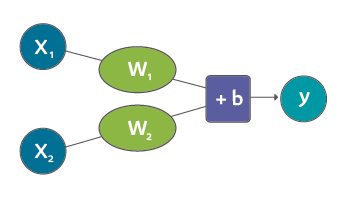
ستبدو شبكتنا العصبونية ذات المتغيرين بهذا الشكل:
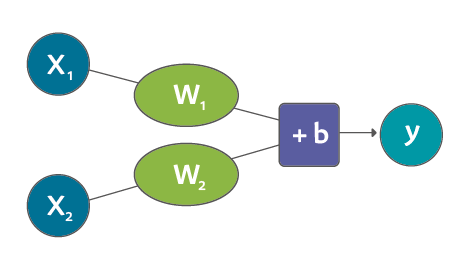
علينا الآن أن نجد وزنين (واحد لكل مدخل) وقيمة انحياز واحدة لإنشاء نموذجنا الجديد.
حساب الدالة Y يبدو كما يلي:

ولكن كيف نجد w1 و w2 ؟ أصبح الأمر أكثر تعقيدًا مقارنة بالسابق عندما كان علينا أن نقلق بشأن قيمة وزن واحدة فقط. ما هو مدى تأثير إضافة متغير "دورة مياه" على توقعنا لقيمة المنزل؟
حاول معرفة قيمة الوزن وقيمة الانحياز الصحيحة. ستبدأ هنا بملاحظة تعقيداتٍ بسبب زيادة عدد مدخلاتنا. إذ سنفقد القدرة على صنع أشكال بسيطة ثنائية الأبعاد تسمح لنا بتصور النموذج للوهلة الأولى. بدلًا من ذلك، سيكون علينا الاعتماد بشكل رئيسي على كيفية تطوير قيمة الخطأ أثناء قيامنا بتعديل العامل المتغير في النموذج.
هنا، سنعتمد على الانحدار المتدرج لمساعدتنا مرة أخرى، إذ لايزال قيّمًا لمساعدتنا في العثور على الأوزان الصحيحة والتحيز.
الآن وبعد أن رأيت الشبكات العصبونية ذات الميزة الواحدة والميزتين، فبإمكانك -نوعًا ما- اكتشاف كيفية إضافة ميزات أخرى واستخدامها لحساب توقعاتك. إذ ستستمر قيمة الوزن في النمو، وسيتعين علينا حينها تعديل تطبيقنا للانحدار المتدرج كلما أضفنا ميزة حتى يتمكن من تحديث الأوزان الجديدة المرتبطة بالميزة الجديدة.
من المهم هنا الانتباه لضرورة عدم إدخال كل ما نعرفه عن أمثلتنا في الشبكة، بل علينا أن نكون انتقائيين حيال الميزات التي نضعها في النموذج. إن اختيار الميزات/المعالجة هو تخصص كامل له مجموعة من الممارسات السليمة والاعتبارات الخاصة به. إذا كنت تريد أن ترى مثالًا لعملية فحص مجموعة بيانات لاختيار الميزات التي تغذي نموذج التوقع، فعليك بقراءة A Journey Through Titanic رحلة عبر تيتانيك، وهو عبارة عن دفتر ملاحظات يروي فيه عمر الجابري طريقته لحل تحدي تيتانيك الذي وضعه Kaggle. حيث يعرض Kaggle مجموعة من البيانات عن معلومات الركاب على متن تيتانك كأسمائهم وجنسهم وأعمارهم ومقصوراتهم لتدريب مجموعة من المصنفات؛ ويكمن التحدي في بناء نموذجٍ يتنبأ بما إذا كان الشخص قد نجا أم لا بالنظر إلى معلوماته الأخرى.
التصنيف
لنواصل تعديل مثالنا، افرض أن صديقك أعطاك قائمة منازل، وأخبرك هذه المرة أنه قام بتصنيفهم حسب رأيه بملاءمة المساحة وعدد دورات المياه:
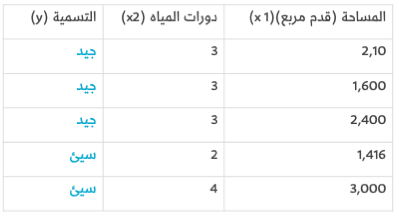
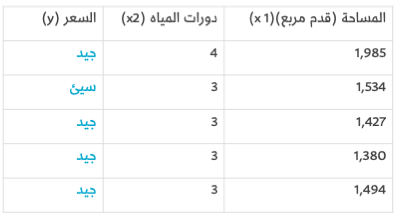
سيطلب منك استخدام هذه القائمة لإنشاء نموذج يتنبأ بما إذا كان سيرغب في أحد المنازل أم لا نظرًا لحجمه وعدد دورات المياه فيه، حينها ستستخدم القائمة أعلاه لبناء نموذج، يمكنه فيما بعد أن يستخدمه لتصنيف العديد من المنازل الأخرى. ولكن هنالك تغييرٌ إضافي واحد في هذه العملية، وهو أنه احتفظ بقائمة أخرى من 10 منازل قام أيضًا بتصنيفها، لكنه أخفاها عنك، سيستخدمها لاحقًا لتقييم النموذج الذي أنشأته بعد تدريبه وتحسينه - في محاولة لضمان أن نموذجك يفهم الشروط التي ستجعله معجبًا بمواصفات المنزل.
جميع الشبكات العصبونية التي ناقشناها حتى الآن تمثل "الانحدار" - لأنها تحسب وتُخرج قيمة "مستمرة" (الإخراج يمكن أن يكون 4 أو 100.6 أو 2143.342343). ولكن في الممارسة العملية، تُستخدم الشبكات العصبونية في كثير من الأحيان في مسائل النوع "التصنيف". في هذه المسائل، يجب أن تكون مُخرجات أو نواتج الشبكة العصبونية قيمة من مجموعة من القيم المنفصلة (أو الطبقات) مثل "جيد" أو "سيئ". ونرى تطبيق ذلك في الممارسة العملية باستحداث نموذجٍ على يقين بنسبة 75٪ أن المنزل الذي وقع عليه الاختيار فعلًا "جيد" بدلًا من مجرد تصنيفه "جيد" أو "سيئ".
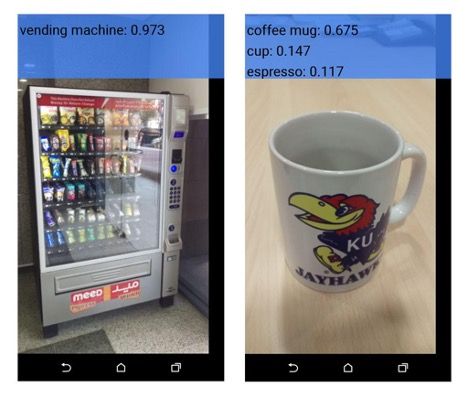 تطبيق TensorFlow الذي ناقشته في المقال السابق يعد مثالًا جيدًا لنماذج التصنيف في الممارسة العملية.
تطبيق TensorFlow الذي ناقشته في المقال السابق يعد مثالًا جيدًا لنماذج التصنيف في الممارسة العملية.
إحدى الطرق التي يمكننا بها تحويل الشبكة التي رأيناها إلى شبكة تصنيف هي إخراج قيمتين - واحدة لكل فئة (فئاتنا الآن هي "جيد" و"سيئ") ثم تمرير هذه القيم عبر عملية تسمى "softmax" ومُخرج softmax هو احتمالية كل فئة. على سبيل المثال، لنفرض أن طبقة من مخرجات الشبكة هي 2 لـ "جيد" و4 لـ "سيئ"، إذا قمنا بإدخال [2، 4] إلى softmax فإنها ستعيد [0.11، 0.88] كمُخرج. وتترجم هذه القيم لتعني أن الشبكة على يقين بنسبة 88٪ من أن القيمة المدخلة هي "سيئ" وصديقتنا لن تحب هذا المنزل.
تأخذ Softmax مصفوفة وتخرج مصفوفة بنفس الطول، لاحظ أن كل مُخرجاتها موجبة ومجموعها يصل إلى 1 ما يُعد أمرًا مفيدًا عندما نقوم بإخراج قيمة احتمالية. لاحظ أيضًا أنه على الرغم من أن 4 هي ضعف 2، فإن احتمالها ليس ضعفًا فحسب، بل هو ثمانية أضعاف احتمال 2 وهذه خاصية مفيدة تضخم الاختلاف في المخرجات وبالتالي تحسن عملية التدريب
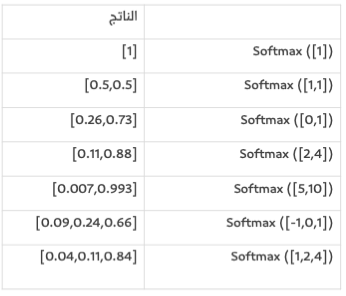
كما ترى في الصفين الأخيرين فإن softmax يمتد لأي عدد من المدخلات. لذا، إذا أضاف صديقنا الآن تصنيفًا ثالثًا (لنفرض: "جيد، لكن سأضطر لتأجير غرفة واحدة")، فإن معايير softmax باستطاعتها أن تكيف مع هذا التغيير.
خذ ثانية لاستكشاف شكل الشبكة عند تغيير عدد الميزات (x1، x2 ، x3 ... إلخ) (كالمساحة، وعدد الحمامات، والسعر، والقرب من المدارس / العمل ... إلخ) وتغيير عدد من الفئات (y1، y2، y3 ... إلخ) (كأن تكون "باهظة الثمن" ، "صفقة جيدة" ، "جيدة إذا كانت airbnb" ، "صغيرة جدًا"):
الميزات (x):
الفئات (y):
X1X2W1,1W2,1W1,2W2,2Y1Y2+b1+b2softmax
يمكنك أن ترى مثالًا على كيفية إنشاء وتهذيب هذه الشبكة باستخدام TensorFlow في هذا المرجع الذي كتبته ليرافق هذا المقال.
الهدف الأساسي
إذا كنت قد وصلت إلى هذه الفقرة، فيجب أن أكشف لك عن الدافع الآخر لكتابة هذا المقال، يُقصد بهذا المقال أن يكون مقدمة لطيفة إلى دروس TensorFlow. في حال بدأت من خلال MNIST For ML Beginners ، وصادفك هذا الرسم البياني لاحقًا:
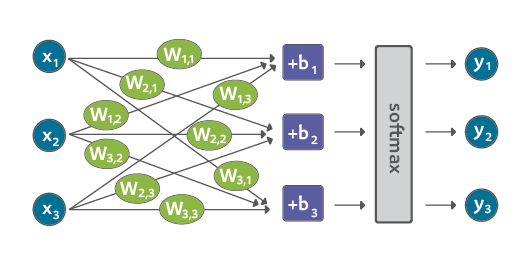 لقد كتبت هذا المنشور لإعداد الأشخاص الذين ليس لديهم خبرة في التعلم الآلي لهذا الرسم البياني في البرنامج التعليمي التمهيدي TensorFlow. لهذا قمت بمحاكاة أسلوبه البصري.
لقد كتبت هذا المنشور لإعداد الأشخاص الذين ليس لديهم خبرة في التعلم الآلي لهذا الرسم البياني في البرنامج التعليمي التمهيدي TensorFlow. لهذا قمت بمحاكاة أسلوبه البصري.
آمل أن تشعر بالتأهب وأن لديك فهم لهذا النظام وكيفية عمله.
يجب عليك أيضًا مواصلة تعليمك عبر تعلم الأسس النظرية والرياضية للمفاهيم التي ناقشنا هنا.
بعض الأسئلة الجيدة التي عليك طرحها الآن تتضمن ما يلي: ● هل توجد أنواعٌ أخرى من دوال التكلفة؟ وأيّها الأفضل لكل تطبيق؟
● ما هي الخوارزمية الأنسب لحساب قيمة الأوزان الجديدة باستخدام الانحدار المتدرج؟
● ما هي تطبيقات التعلم الآلي في المجالات التي تعرفها بالفعل؟ ماذا يمكنك أن تصنع باستخدام هذه المعارف الجديدة ودمجها بمعلوماتك السابقة؟
● Coursera’s Machine Learning course by Andrew Ng. This is the one I started with. Starts with regression then moves to classification and neural networks.
● Coursera’s Neural Networks for Machine Learning by Geoffrey Hinton. More focused on neural networks and its visual applications.
● Stanford’s CS231n: Convolutional Neural Networks for Visual Recognition by Andrej Karpathy. It’s interesting to see some advanced concepts and the state of the art in visual recognition using deep neural networks.
● The Neural Network Zoo is a great resource to learn more about the different types of neural networks.
كتابة جهاد العمار، ترجمة مركز ذكاء ونجلاء العريفي